그리디 문제입니다.
문제를 요약하면 다음과 같습니다.
N개를 P 묶음으로 나누고, 각 묶음의 곱이 최대가 되게 하라.
만약 P가 3이게 된다면 아래와 같은 식이 도출될 수 있습니다.
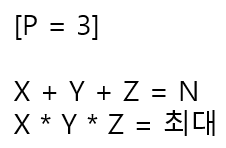
합이 일정할 때, 곱을 최대로 하려면 어떻게 해야 할까요?
각 원소의 차이를 최소로 하면 됩니다.
N = 8, P = 3 일 때, 아래와 같이 달란트 묶임이 만들어집니다.
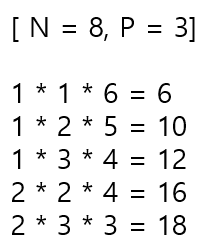
(2, 3, 3) 과 같이 그 차이가 최소로 만들 때 곱이 최대가 됩니다.
[구현 코드]
import java.util.*;
import java.io.*;
public class Solution {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stz;
int t = Integer.parseInt(br.readLine());
for (int testCase = 1; testCase <= t; testCase++) {
stz = new StringTokenizer(br.readLine());
int n = Integer.parseInt(stz.nextToken());
int p = Integer.parseInt(stz.nextToken());
// 각 원소의 차이가 최소를 만들 때, p로 나눈 몫이 최소
int di = n / p;
int re = n % p;
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < p; i++) {
int value = di;
// 나머지가 있을 때, 원소에 1씩 더해서 남는 것이 없도록 함
if (re-- > 0) {
value++;
}
map.put(value, map.getOrDefault(value, 0) + 1);
}
// 타입 주의!
long mul = 1;
for (int key : map.keySet()) {
mul *= Math.pow((long) key, (long) map.get(key));
}
System.out.printf("#%d %d" + System.lineSeparator(), testCase, mul);
}
}
}'알고리즘' 카테고리의 다른 글
| 백준 - 17825 주사위 윷놀이 (Java) (0) | 2023.07.25 |
|---|---|
| 백준 - 17822 원판 돌리기 (0) | 2023.07.22 |
| SW Expert - 1812 수정이의 타일 자르기(Java) (0) | 2023.07.17 |
| SW Expert - 1267 작업 순서 (0) | 2023.07.16 |
| 백준 - 1339 단어 수학(Java) (0) | 2023.06.06 |



