구현 문제입니다.
이 문제는 약수의 개수를 통해 해결하는 문제입니다.
왜 약수의 개수의 문제를 구해야 하는지 알아보겠습니다.
이 문제의 접근은 세 단계로 이뤄집니다.
- 왜 약수인가?
- 약수의 개수 구하기
- 범위 내 최대 약수의 개수 (중요!)
1. 왜 약수인가?
영우는 s와 e가 주어질 때, "s<= x <=e"를 만족하는 수 중에서 억억단에 가장 많이 등장한 수를 구해야 합니다.
s=1, e=8 일 때의 그림을 보겠습니다

그림에서 등장한 수를 세어 보겠습니다.
1은 1번 등장했습니다.
2는 2번 등장했습니다.
3은 2번 등장했습니다.
4는 3번 등장했습니다.
5는 2번 등장했습니다.
6은 4번 등장했습니다.
7은 2번 등장했습니다.
8번 4번 등장했습니다.
가장 많이 등장한 수는 6과 8입니다.
이 중에서 가장 작은 수인 6이 정답입니다.
눈치 채신 분들이 있겠지만, 각 수의 등장은 해당 수의 약수의 개수와 같습니다.
1의 약수는 {1}로 1개 입니다.
2의 약수는 {1,2}로 2개 입니다.
3의 약수는 {1,3}로 3개 입니다.
4의 약수는 {1,2,4}로 3개 입니다.
5의 약수는 {1,5}로 2개 입니다.
6의 약수는 {1,2,3,6}로 4개 입니다.
7의 약수는 {1,7}로 2개 입니다.
8의 약수는 {1,2,4,8}로 4개 입니다.
위 이유로 약수의 개수를 구해야 하는 것을 알 수 있습니다.
2. 약수의 개수 구하기
중학생 때, 약수의 개수는 소인수 분해를 통해 구할 수 있음을 배운적이 있습니다.
(물론, 저는 까먹어서 인터넷에 공식을 찾아봤습니다...)
예를 들어 설명하겠습니다.
12의 약수의 {1, 2, 3, 4, 6, 12}로 6개 입니다.
12를 소인수 분해하면 다음 그림과 같습니다.

이를 식으로 나타내면
12 = 2² * 3¹ 입니다.
즉, 다음 표와 같습니다.

이를 공식화 시키면
다음과 같습니다.
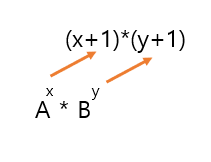
이를 예시에 적용하면 다음과 같습니다.

만약 세 개의 곱 이상으로 이루어 진다해도 식은 성립합니다.
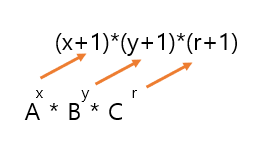
3. 범위 내 최대 약수의 개수
2번까지 설명을 통해 약수의 개수를 구해야 하는 이유와, 그 방법을 알아봤습니다.
때문에, 2번 까지만 보고 문제를 풀 수는 있겠지만, 아쉽게도 7번 또는 8번부터 시간초과가 발생할 것입니다.
이 문제의 입력 범위가 너무 넓기 때문에, starts만큼 반복하여 소수의 개수를 구하는 방법을 사용해서는 안됩니다.
문제에서 요구하는 것은 여러 개의 s 부터 한 개의 e까지 범위 사이에서 공약수의 개수를 최대인 수를 구하는 것입니다.
이를 반대로 생각하면 e 부터 1까지 최대 약수의 수를 가진 수를 갱신 및 저장하여 s의 위치를 배열에서 찾아내면 됩니다.
말로 설명하기에는 제 서술 능력이 부족하여 예제의 그림을 통해 설명하겠습니다.
문제의 예제는 e=1, starts=[1, 3, 7]입니다.
즉, 1~8, 3~8, 7~8 사이의 수에서 약수의 수를 최대로 가지는 수를 구하는 것입니다.
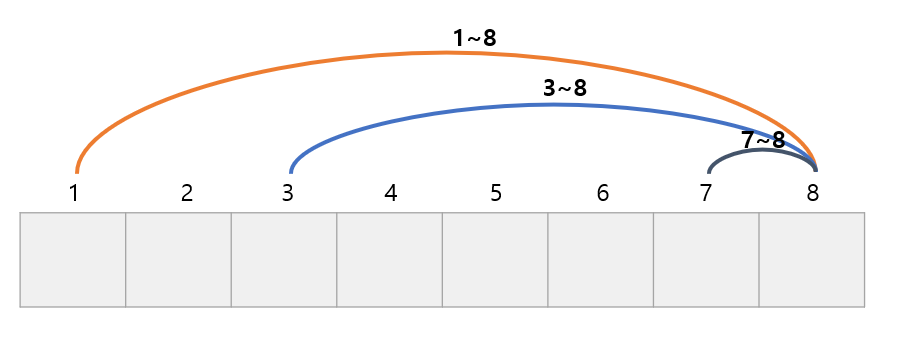
각 위치 약수의 개수 구하면 다음과 같습니다.

거의 다 끝났습니다.
위에서 한 번 설명했듯이, e 부터 starts까지의 최대 약수의 수를 갱신시켜 보겠습니다.
끝인 8부터 시작하여 최대의 값과 그 위치를 저장합니다.
뒤에서 앞으로 가면서 최대를 갱신합니다.
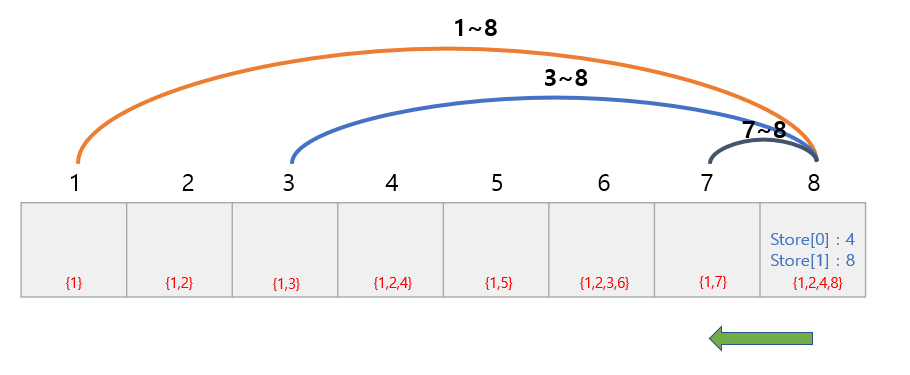
만약 같은 약수의 개수를 가진 수가 나타나도 갱신을 해야 합니다.
이유는, 문제 조건에 "가장 많이 등장한 수가 여러개라면 그 중 가장 작은수를 답해야 합니다."가 있기 때문입니다.

문제 조건에 의해 6과 8은 각각 네 개의 약수를 가지고 있지만, 6위치에서 갱신되어야 합니다.
store[0]은 최대 약수의 개수를 저장합니다.
store[1]은 그 숫자를 저장합니다.
starts = {1, 3, 7}는 위 저장된 store 배열에서 값을 가져오면 됩니다.
문제에서 요구하는 것은 개수가 아닌 최대 약수를 가진 수를 가져오는 것이기 때문에, store[1]위치의 값을 가져와야 합니다.
(그림에서 편의상 1차원 배열로 표현했지만, 실제로는 이차원 배열를 사용해 저장해야 합니다.)
strats[1] = store[1][1] = 6
strats[3] = store[3][1] = 6
strats[3] = store[7][1] = 8
인 것을 알 수 있습니다.
[구현 코드]
import java.util.*;
class Solution {
public static int[] solution(int e, int[] starts) {
int[] answer = new int[starts.length];
/*
* "e 부터" 시작하여 1까지 최대 약수의 개수를 저장함
* [0] : 최대 약수의 개수
* [1] : 최대 약수의 위치
* */
int[][] store = new int[e+1][2];
store[e][0] = primeCount(e);
store[e][1] = e;
for(int i=e-1; i>=1; i--){
int cnt = primeCount(i);
// 최대 약수 갱신
if(cnt >= store[i+1][0]){
store[i][0] = cnt;
store[i][1] = i;
}else{
store[i][0] = store[i+1][0];
store[i][1] = store[i+1][1];
}
}
for (int i = 0; i < starts.length; i++) {
int star = starts[i];
answer[i] = store[star][1];
}
return answer;
}
// 소수의 개수
private static int primeCount(int n) {
/*
* primes의 key는 밑이고, value는 지수
* 2³일 경우 key : 2, value : 3
* 약수의 개수를 구하는 공식을 사용하기 위해, primes에 지수를 저장
* */
Map<Integer, Integer> primes = new HashMap<>();
for (int i = 2; i <= Math.sqrt(n); i++) {
while (n % i == 0) {
primes.put(i, primes.getOrDefault(i, 0) + 1);
n /= i;
}
}
if (n != 1) {
primes.put(n, primes.getOrDefault(n, 0) + 1);
}
int count = 1;
List<Map.Entry<Integer, Integer>> list = new ArrayList<>(primes.entrySet());
for (Map.Entry<Integer, Integer> entry : list) {
count *= (entry.getValue() + 1);
}
return count;
}
}'알고리즘' 카테고리의 다른 글
| 프로그래머스 - 디펜스 게임(Java) (7) | 2022.12.11 |
|---|---|
| 프로그래머스 - 점 찍기(Java) (0) | 2022.12.02 |
| 프로그래머스 - 귤 고르기(Java) (0) | 2022.11.30 |
| 백준 - 1865 웜홀(Java) (0) | 2022.11.30 |
| 백준 - 5639 이진 검색 트리(Java) (0) | 2022.11.30 |



