https://www.acmicpc.net/problem/21921
21921번: 블로그
첫째 줄에 $X$일 동안 가장 많이 들어온 방문자 수를 출력한다. 만약 최대 방문자 수가 0명이라면 SAD를 출력한다. 만약 최대 방문자 수가 0명이 아닌 경우 둘째 줄에 기간이 몇 개 있는지 출력한다
www.acmicpc.net
누적합 문제입니다.
일정 범위가 주어졌을 때, 최대 누적합과 그 개수를 구하는 문제입니다.
예를 들어 설명하겠습니다.
{1, 4, 2, 5, 1} 배열이 있고 구간의 크기가 2라고 했을 때 최대 누적합은 7이며 그 개수는 1개 입니다.
{1, 1, 1, 1, 1, 5, 1}배열이 있고 구간의 크기가 5라고 했을 때 최대 누적합은 9이며 그 개수는 2개 입니다.
시간 복잡도가 O(N^2)인 반복문은 N의 개수가 250,000까지 주어지기 때문에250,000^2 = 62,500,000,000으로 사용해서는 안됩니다.
이를 O(N)으로 줄일 수 있는 방법이 있는데, 그것은 투포인터의 변형이라 할 수 있는 슬라이더 입니다.
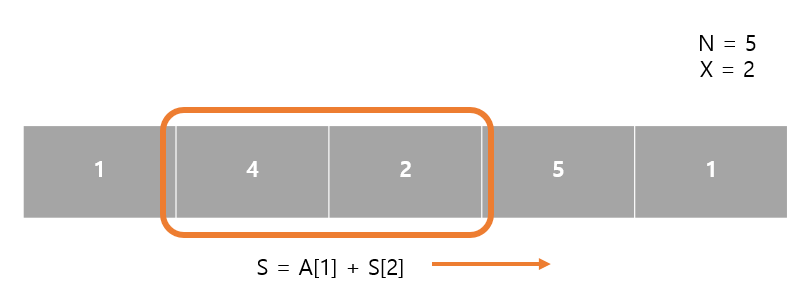
그림과 같이 특정 크기를 가지는 슬라이더를 움직이면서 구간 합의 최대를 구하면 됩니다.
반복문 한 번만 쓰면 되기 때문에 시간 복잡도가 O(N)으로 줄어들게 됩니다.
그림의 슬라이더가 한 번 움직이면 S = S - A[1] + A[3]가 되는 것입니다.
이런 방식으로 슬라이더끝이 배열의 끝까지 도달하면 반복문을 끝내면 됩니다.
[구현 코드]
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer stz = new StringTokenizer(br.readLine()," ");
int n = Integer.parseInt(stz.nextToken());
int x = Integer.parseInt(stz.nextToken());
int[] arr = new int[n];
stz = new StringTokenizer(br.readLine(), " ");
for (int i = 0; i < n; i++) {
arr[i] = Integer.parseInt(stz.nextToken());
}
// 첫 부분합
long pSum = 0;
for (int i = 0; i < x; i++) {
pSum += arr[i];
}
int cnt = 1;
long ans = pSum;
for(int i=x; i<n; i++){
pSum += (arr[i] - arr[i-x]);
if(ans == pSum){
cnt++;
}else if(pSum > ans){
cnt = 1;
ans = pSum;
}
}
if(ans == 0){
bw.write("SAD");
}else {
bw.write(ans + "\n" + cnt);
}
bw.flush();
bw.close();
br.close();
}
}
'알고리즘' 카테고리의 다른 글
| 백준 - 1644 소수의 연속합(Java) (0) | 2022.09.16 |
|---|---|
| 백준 - 2470 두 용액(Java) (0) | 2022.09.16 |
| 백준 - 2110 공유기 설치(Java) (0) | 2022.09.15 |
| 백준 - 1629 곱셈(Java) (0) | 2022.09.15 |
| 백준 - 12865 평범한 배낭(Java) (0) | 2022.09.14 |



