https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
DP 문제입니다.
특정 수열이 주어졌을 때, 해당 수열 안에서 오름 차순으로 증가하면서 가장 긴 부분 수열 길이를 찾는 문제입니다.
예를 들어 {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 으로 길이는 4 입니다.(볼드체로 강조 된 부분이 가장 긴 부분 수열의 원소들 입니다)
문제 풀이의 핵심은 현재 위치에서 이전의 것을 비교하여 부분 수열을 찾아야 합니다.즉, 현재의 위치가 부분 수열의 최대일 때의 부분 수열 길이를 구하는 문제로 생각해야 합니다.
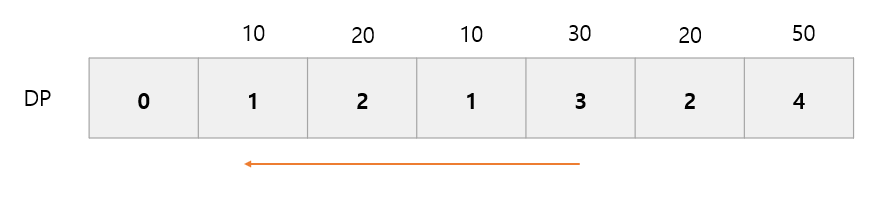
그림의 dp[4]의 값은 {10, 20, 10, 30} 부분 수열에서 자신 보다 작은 부분 수열 원소들을 확인해 갱신 한 것입니다.
즉, 점화식은 dp[i] = max(dp[0], dp[1], dp[2], ..., dp[i-1]) + 1 입니다.
(+1을 한 이유는 자기 자신 역시 부분 수열에 포함되게 하기 위함 입니다.)
[구현 코드]
import java.io.*;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
private static int[] arr, dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer stz;
int n = Integer.parseInt(br.readLine());
arr = new int[n + 1];
dp = new int[n + 1];
stz = new StringTokenizer(br.readLine(), " ");
for (int i = 1; i < n + 1; i++) {
arr[i] = Integer.parseInt(stz.nextToken());
}
Arrays.fill(dp, -1);
// 각 배열의 시점을 기준으로 이전을 보면서 가장 긴 부분 증가 수열을 찾음
for (int i = 1; i < n+1; i++) {
dp[i] = lis(i);
}
int ans = 0;
for (int i = 1; i < n+1; i++) {
ans = Math.max(ans, dp[i]);
}
bw.write(String.valueOf(ans));
bw.flush();
bw.close();
br.close();
}
private static int lis(int i) {
// memorization을 하여 이미 탐색 한 부분을 다시 탐색 하지 않도록 함
// 아직 탐색을 하지 않았다면
if(dp[i]== -1){
// 자기 자신만 포함된 수열의 길이는 1이기 때문에 최소는 1임
dp[i] = 1;
// 현재를 기준으로 이전의 것을 볼 거임
for(int j=i; j>=1; j--){
// 현재 자신 보다 작은 것을 찾음
if(arr[j] < arr[i]) {
dp[i] = Math.max(dp[i], lis(j) + 1);
}
}
}
return dp[i];
}
}'알고리즘' 카테고리의 다른 글
| 백준 - 1629 곱셈(Java) (0) | 2022.09.15 |
|---|---|
| 백준 - 12865 평범한 배낭(Java) (0) | 2022.09.14 |
| 백준 - 2579 계단 오르기(Java) (0) | 2022.09.14 |
| 백준 - 1932 정수 삼각형(Java) (0) | 2022.09.14 |
| 백준 - 15661 링크와 스타트(Java) (0) | 2022.09.13 |



